A Lisp Interpreter Implemented in Conway's Game of Life
Lisp in Life is a Lisp interpreter implemented in Conway’s Game of Life.
The entire pattern is viewable on the browser here.
To the best of my knowledge, this is the first time a high-level programming language was interpreted in Conway’s Game of Life.
Running Lisp on the Game of Life
Lisp is a language with a simple and elegant design, having an extensive ability to express sophisticated ideas as simple programs. Notably, the powerful feature of macros could be used to modify the language’s syntax to write programs in a highly flexible way. For example, macros can be used to introduce new programming paradigms to the language, as demonstrated in object-oriented-like.lisp (which can actually be evaluated by the interpreter, although complex programs take quite a long time to finish running), where a structure and syntax similar to classes in Object Oriented Programming is constructed. Despite the expressibility of Lisp, it is the world’s second oldest high-level programming language introduced in 1958, only to be preceded by Fortran.
Conway’s Game of Life is a cellular automaton proposed in 1970. Despite it having a very simple set of rules, it is known to be Turing Complete. Lisp in Life demonstrates this fact in a rather straightforward way.
How can simple systems allow human thoughts to be articulated and be expanded? With the expressibility of Lisp and the basis of Conway’s Game of Life, Lisp in Life provides an answer to this question.
Input and Output
The Lisp program is provided by editing certain cells within the pattern to represent the ASCII-encoding of the Lisp program. The pattern directly reads this text and evaluates the results. You can also load your own Lisp program into the pattern and run it. The standard output is written at the bottom end of the RAM module, which can be easily located and directly examined in a Game of Life viewer. The Lisp implementation supports lexical closures and macros, allowing one to write Lisp programs in a Lisp-like taste, as far as the memory limit allows you to.
The Lisp interpreter is written in C. Using the build system for this project, you can also compile your own C11-compatible C code and run in on Conway’s Game of Life.
Previous Work
As previously mentioned, to the best of my knowledge, this is the first time a high-level programming language was interpreted in Conway’s Game of Life.
The entry featuring Universal Computers in LifeWiki has a list of computers created in the Game of Life. Two important instances not mentioned in this entry are the Quest For Tetris (QFT) Project created by the authors of the QFT project, and APGsembly created by Adam P. Goucher. All of these work are designed to run an assembly language and are not designed to interpret a high-level language per se.
An example of a compiled high-level language targeted for the Game of Life is Cogol by the QFT project. Cogol is compiled to the assembly language QFTASM, targeted for the QFT architecture. Although Cogol is targeted for the QFT architecture, it requires compilation to QFTASM for the code to be run in the QFT architecture.
In Lisp in Life, a modified version of the QFT architecture is first created for improving the pattern’s runtime. Modifications include introducing a new cascaded storage architecture for the ROM, new opcodes, extending the ROM and RAM address space, etc. The Lisp source code is then written into the computer’s RAM module as its raw binary ASCII format. The Conway’s Game of Life pattern directly reads, parses, and evaluates this Lisp source code to produce its output. This feature of allowing a Conway’s Game of Life pattern to evaluate a high-level programming language expressed as a string of text is a novel feature that was newly achieved in this project.
Video
Here is a YouTube video showing Lisp in Life in action:
Screenshots

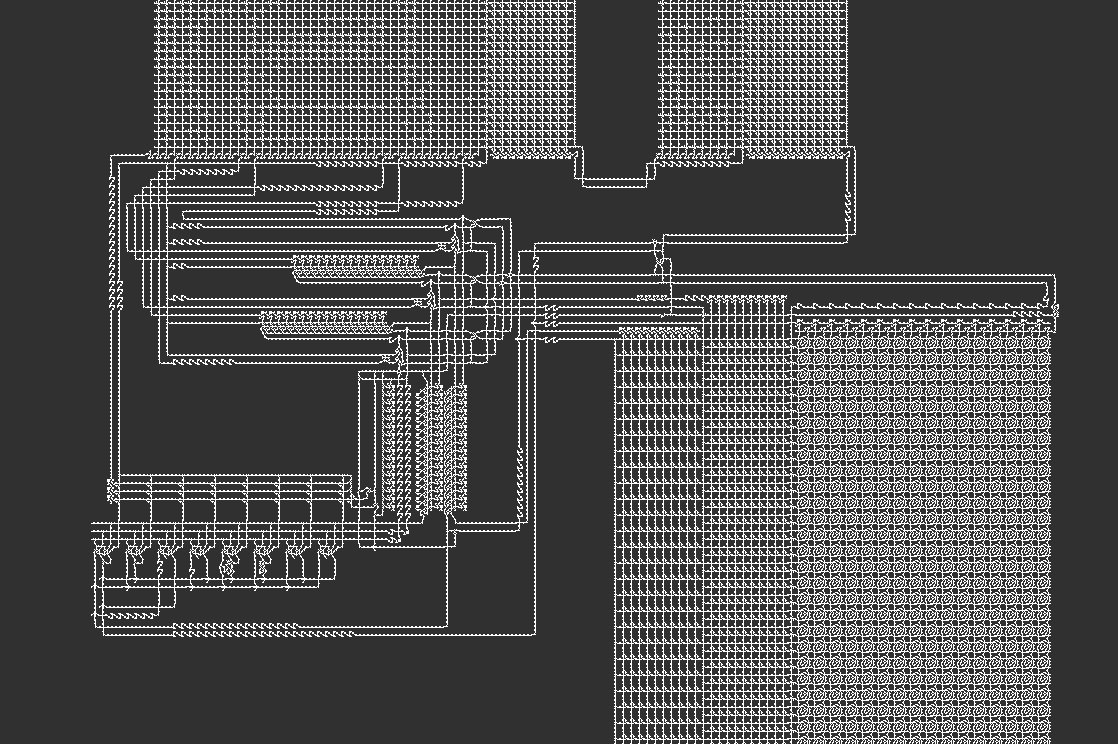
An overview of the entire architecture.

An overview of the CPU and its surrounding modules. On the top are the ROM modules, with the lookup module on the right, and the value modules on the left. On the bottom left is the CPU. On the bottom right is the RAM module.
This pattern is the VarLife version of the architecture. VarLife is an 8-state cellular automaton defined in the Quest For Tetris (QFT) Project, which is used as an intermediate layer to create the final Conway’s Game of Life pattern. The colors of the cells indicate the 8 distinct states of the VarLife rule.
The architecture is based on Tetris8.mc in the original QFT repository. Various modifications were made to make the pattern compact, such as introducing a new lookup table architecture for the ROM, removing and adding new opcodes, expanding the ROM and RAM address space, etc.
The Conway’s Game of Life version of the architecture, converted from the VarLife pattern. What appears to be a single cell in this image is actually an OTCA metapixel zoomed away to be shown 2048 times smaller.
A close-up view of a part of the ROM module in the Conway’s Game of Life version. Each pixel in the previous image is actually this square-shaped structure shown in this image. These structures are OTCA metapixels, which can be seen to be in the On and Off meta-states in this image. The OTCA Metapixel is a special Conway’s Game of Life pattern that can emulate cellular automatons with customized rules. The original VarLife pattern is simulated this way so that it can run in Conway’s Game of Life.
The OTCA Metapixel simulating Life in Life can be seen in this wonderful video by Phillip Bradbury: https://www.youtube.com/watch?v=xP5-iIeKXE8
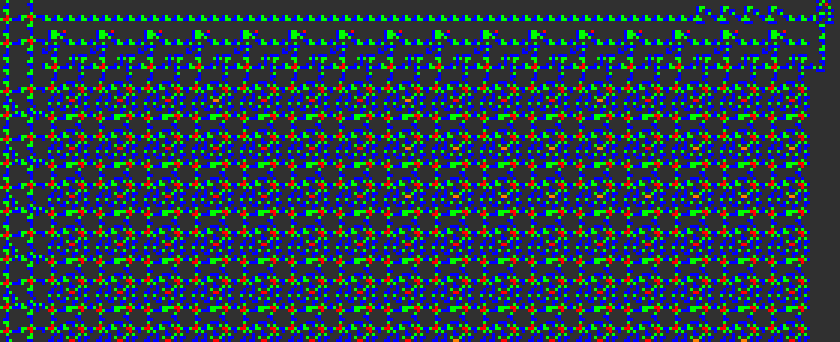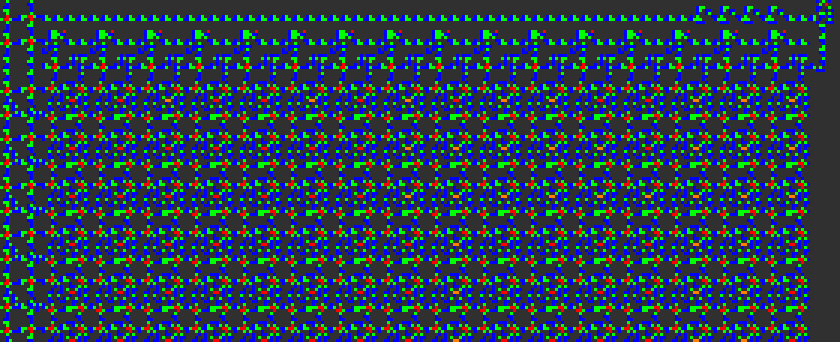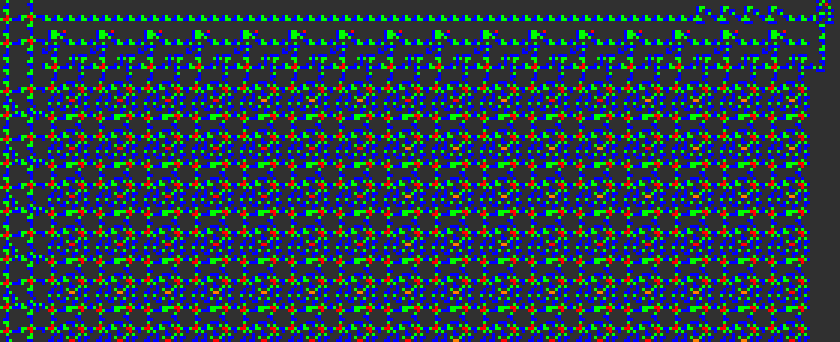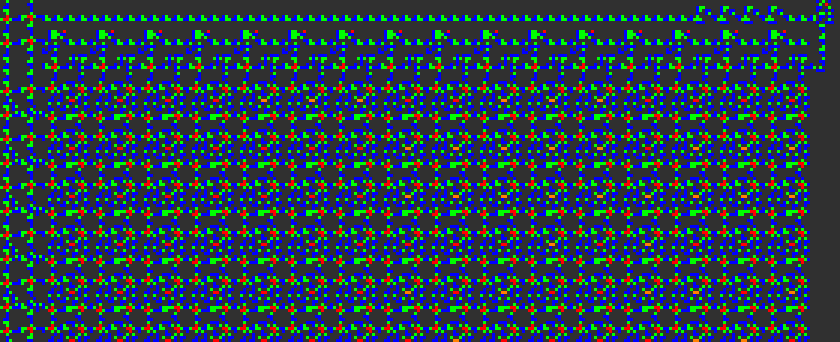
A video of the RAM module in the VarLife rule in action.

The computer showing the results of the following Lisp program:
(define mult (lambda (m n)
(* m n)))
(print (mult 3 14))
The result is 42, shown in binary ascii format (0b110100, 0b110010), read in bottom-to-up order.
As shown in this image, the standard output of the Lisp program gets written at the bottom end of the RAM module, and can be directly viewed in a Game of Life viewer. This repository also contains scripts that run on Golly to decode and view the contents of the output as strings.
How is it Done?
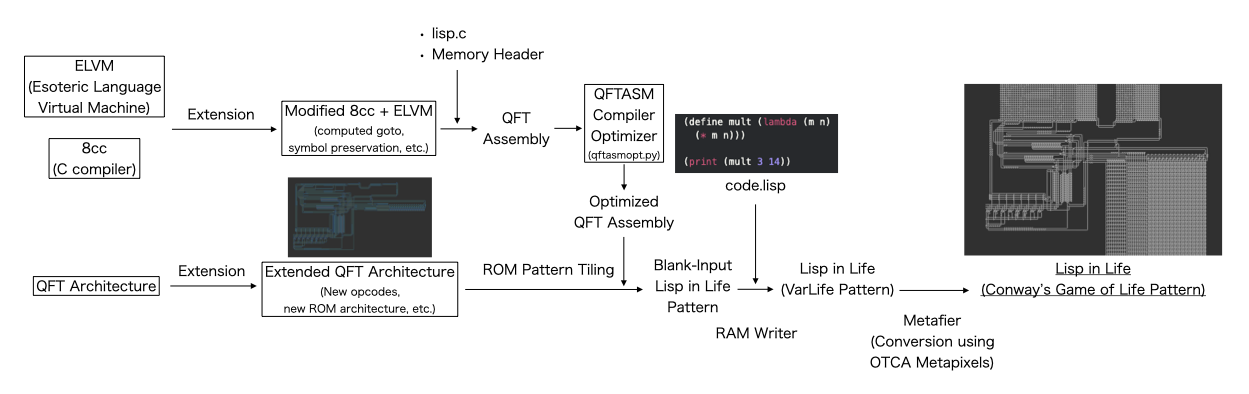
The Lisp interpreter, written in C, is compiled to an assembly language for a CPU architecture implemented in the Game of Life, which is a modification of the computer used in the Quest For Tetris (QFT) project. The compilation is done using an extended version of ELVM (the Esoteric Language Virtual Machine). The Game of Life backend for ELVM was implemented by myself.
Generating a small enough pattern that runs in a reasonable amount of time required a lot of effort. This required optimizations and improvements in every layer of the project; a brief summary would be:
- The C Compiler layer - adding the computed goto feature to the C compiler, preserving variable symbols to be used after compilation, etc.
- The C layer (the Lisp interpreter) - using a string hashtable and binary search for Lisp symbol lookup, minimization of stack region usage with union memory structures, careful memory region map design, etc.
- The QFTASM layer - writing a compiler optimizer to optimize the length of the assembly code
- The VarLife layer (the CPU architecture) - creating a lookup table architecture for faster ROM access, expanding the size and length of the RAM module, adding new opcodes, etc.
- The Game of Life layer - Hashlife-specific optimization
A more detailed description of the optimizations done in this project is available in the Implementation Details section.
Conversion from VarLife to Conway’s Game of Life
VarLife is an 8-state cellular automaton defined in the Quest For Tetris (QFT) Project. It is used as an intermediate layer to generate the final Conway’s Game of Life pattern; the computer is first created in VarLife, and then converted to a Game of Life pattern.
When converting VarLife to Conway’s Game of Life, each VarLife cell is mapped to an OTCA Metapixel (OTCAMP). The conversion from VarLife to the Game of Life is done in a way so that the behavior of the states of the VarLife pattern matches exactly with the meta-states of the OTCA Metapixels in the converted Game of Life pattern. Therefore, it is enough to verify the behavior of the VarLife pattern to verify the behavior of the Game of Life pattern.
Due to the use of OTCA Metapixels, each VarLife cell becomes extended to a 2048x2048 Game of Life cell, and 1 VarLife generation requires 35328 Game of Life generations. Therefore, the VarLife patterns run significantly faster than the Game of Life (GoL) version.
Additional details on VarLife are available in the Miscellaneous section.
Pattern Files
Pattern files preloaded with various Lisp programs are available here. Detailed statistics such as the running time and the memory consumption are available in the Running Times and Statistics section.
The patterns can be simulated on the Game of Life simulator Golly.
The VarLife patterns can be simulated on Golly as well. To run the VarLife patterns, open Golly and see File -> Preferences -> Control, and Check the “Your Rules” directory. Open the directory, and copy https://github.com/woodrush/QFT-devkit/blob/main/QFT-devkit/Varlife.rule to the directory.
Descriptions of the Lisp Programs
-
object-oriented-like.lisp: This example creates a structure similar to classes in Object-Oriented Programming, using closures.
- The class has methods and field variables, where each instance carries distinct and persistent memory locations of their own. The example instantiates two counters and concurrently modifies the value held by each instance.
- New syntaxes for instantiation and method access,
(new classname)and(. instance methodname), are introduced using macros and functions.
The Lisp interpreter’s variable scope and the macro feature is powerful enough to manage complex memory management, and even providing a new syntax to support the target paradigm.
-
printquote.lisp: A simple demonstration of macros.
-
factorial.lisp: A simple demonstration of recursion with the factorial function.
-
z-combinator.lisp: Demonstration of the Z Combinator to implement a factorial function using anonymous recursion.
-
backquote-splice.lisp: Implements the backquote macro used commonly in Lisp to construct macros. It also supports the unquote and unquote-splice operations, each written as
~and~@. -
primes.lisp: Prints a list of prime numbers up to 20. This example highlights the use of the
whilesyntax.
The contents of print.lisp is quite straightforward - it calculates and prints the result of 3 * 14.
backquote.lisp and primes-print.lisp are similar to backquote-splice.lisp and primes.lisp, mainly included for performance comparisons.
backquote.lisp doesn’t implement the unquote-splice operation, and demonstrates some more examples.
primes-print.lisp reduces the number of list operations to save memory usage.
Details of the Lisp Interpreter
Special Forms and Builtin Functions
- define
- if
- quote
- car, cdr
- cons
- list
- atom
- progn
- while
- lambda, macro
- eval
- eq
- +, -, *, /, mod, <, >
Lexical Closures
This Lisp interpreter supports lexical closures. The implementation of lexical closures is powerful enough to write an object-oriented-like code as shown in object-oriented-like.lisp, where classes are represented as lexical closures over the field variables and the class methods.
Macros
This Lisp interpreter supports macros. Lisp macros can be thought as a function that receives code and returns code. Following this design, macros are treated exacly the same as lambdas, except that it takes the arguments as raw S-expressions, and evaluates the result twice (the first time to build the expression, and the second time to actually evaluate the builded expression).
Running Times and Statistics
VarLife Patterns
| Lisp Program and Pattern (VarLife) | #Halting Generations (VarLife) | Running Time (VarLife) | Memory Usage (VarLife) |
|---|---|---|---|
| print.lisp [pattern] | 105,413,068 (exact) | 1.159 mins | 5.0 GiB |
| lambda.lisp [pattern] | 700,000,000 | 2.966 mins | 12.5 GiB |
| printquote.lisp [pattern] | 800,000,000 | 3.424 mins | 12.5 GiB |
| factorial.lisp [pattern] | 1,000,000,000 | 5.200 mins | 17.9 GiB |
| z-combinator.lisp [pattern] | 1,700,000,000 | 9.823 mins | 23.4 GiB |
| backquote-splice.lisp [pattern] | 4,100,000,000 | 20.467 mins | 27.5 GiB (max.) |
| backquote.lisp [pattern] | 4,100,000,000 | 21.663 mins | 27.5 GiB (max.) |
| object-oriented-like.lisp [pattern] | 4,673,000,000 | 22.363 mins | 27.5 GiB (max.) |
| primes-print.lisp [pattern] | 8,880,000,000 | 27.543 mins | 27.5 GiB (max.) |
| primes.lisp [pattern] | 9,607,100,000 | 38.334 mins | 27.5 GiB (max.) |
Conway’s Game of Life (GoL) Patterns
| Lisp Program and Pattern (GoL) | #Halting Generations (GoL) | Running Time (GoL) | Memory Usage (GoL) |
|---|---|---|---|
| print.lisp [pattern] | 3,724,032,866,304 | 382.415 mins | 27.5 GiB (max.) |
| lambda.lisp [pattern] | 24,729,600,000,000 | 1372.985 mins | 27.5 GiB (max.) |
| printquote.lisp [pattern] | 28,262,400,000,000 | 1938.455 mins | 27.5 GiB (max.) |
| factorial.lisp [pattern] | 35,328,000,000,000 | 3395.371 mins | 27.5 GiB (max.) |
| z-combinator.lisp [pattern] | 60,057,600,000,000 | - | - |
| backquote-splice.lisp [pattern] | 144,844,800,000,000 | - | - |
| backquote.lisp [pattern] | 144,844,800,000,000 | - | - |
| object-oriented-like.lisp [pattern] | 165,087,744,000,000 | - | - |
| primes-print.lisp [pattern] | 313,712,640,000,000 | - | - |
| primes.lisp [pattern] | 339,399,628,800,000 | - | - |
Common Statistics
| Lisp Program | #QFT CPU Cycles | QFT RAM Usage (Words) |
|---|---|---|
| print.lisp | 4,425 | 92 |
| lambda.lisp | 13,814 | 227 |
| printquote.lisp | 18,730 | 271 |
| factorial.lisp | 28,623 | 371 |
| z-combinator.lisp | 58,883 | 544 |
| backquote-splice.lisp | 142,353 | 869 |
| backquote.lisp | 142,742 | 876 |
| object-oriented-like.lisp | 161,843 | 838 |
| primes-print.lisp | 281,883 | 527 |
| primes.lisp | 304,964 | 943 |
The running times for each program are shown above. The Hashlife algorithm used for the simulation requires a lot of memory in exchange of speedups. The simulations were run on a 32GB-RAM computer, with Golly’s memory usage limit set to 28000 MB, and the default base step to 2 (configurable from the preferences). The memory usage was measured by Ubuntu’s activity monitor. “(max.)” shows where the maximum permitted memory was used. The number of CPU cycles and the QFT memory usage was obtained by running the QFTASM interpreter on the host PC. The QFT memory usage shows the number of RAM addresses that were written at least once. The memory usage is measured in words, which is 16 bits in this architecture.
All of the VarLife patterns can actually be run on a computer. The shortest running time is about 1 minute for print.lisp. A sophisticated program such as object-oriented-like.lisp can even run in about 22 minutes.
On the other hand, the Game of Life patterns take significantly more time than the VarLife patterns, but for short programs it can be run in a moderately reasonable amount of time. For example, print.lisp finishes running in about 6 hours in the Game of Life pattern. As mentioned in the “Conversion from VarLife to Conway’s Game of Life” section, since the Game of Life pattern emulates the behavior of the VarLife pattern using OTCA Metapixels, the behavior of the Game of Life patterns can be verified by running the VarLife patterns.
Tests
There are tests to check the behavior of the Lisp interpreter. There is a test for checking the QFTASM-compiled Lisp interpreter using the QFTASM interpreter, and a test for checking the GCC-compiled Lisp interpreter on the host pc. To run these tests, use the following commands:
git submodule update --init --recursive # Required for building the source
make test # Run the tests for the QFTASM-compiled Lisp interpreter, using the QFTASM interpreter
make test_executable # Run the tests for the executable compiled by GCC
Running make test requires Hy, a Clojure-like Lisp implemented in Python available via pip install hy.
Some of the tests compare the output results of Hy and the output of the QFTASM Lisp interpreter.
The tests were run on Ubuntu and Mac.
Building from Source
This section explains how to load the Lisp interpreter (written in C) to the Game of Life pattern, and also how to load a custom Lisp program into the pattern to run it on Game of Life.
Please see build.md from the GitHub repository.
Implementation Details
This section describes the implementation details for the various optimizations for the QFT assembly and the resulting Game of Life pattern.
The C Compiler layer
- Added the computed goto feature to ELVM
- This was merged into the original ELVM project.
- Modified the compiler to preserve and output memory address symbols and program address symbols, for their usage in the compiler optimization tool in the QFTASM layer
- This allows to use memheader.eir, so that symbols used in the C source can be referenced in the ELVM assembly layer using the same variable symbols.
The ELVM Assembly layer
- Wrote the QFTASM backend for ELVM
- This was merged into the original ELVM project.
- Added further improvements to the QFTASM backend:
- Let the ELVM assembly’s memory address space match QFT’s native memory address space
- Originally, the ELVM assembly had to convert its memory address every time when a memory access occurs.
- Support new opcodes added in the improved QFT architecture
- Let the ELVM assembly’s memory address space match QFT’s native memory address space
The C layer (the implementation of the Lisp interpreter)
Usage of binary search and hashtables for string representations and comparisons
By profiling the GCC-compiled version of the Lisp interpreter, it was found that the string table lookup process was a large performance bottleneck. This was a large room for optimization.
The optimized string lookup process is as follows. First, when the Lisp parser accepts a symbol token, it creates a 4-bit hash of the string with the checksum of the ASCII representation of the string. The hash points to a hashtable that holds the root of a binary search tree for string comparison. Each node in the tree holds the string of the symbol token, and two nodes that are before and after the token in alphabetical order. When a query symbol token arrives in the parsing phase, a node with a matching token is returned, or a new node for the token is added into this binary tree if the token does not exist yet. This allows for each distinct symbol in the S-expression to have a distinct memory address.
In the interpretation phase, since each distinct symbol has a distinct memory address, and every string required for the Lisp program has already been parsed, string comparison can be done by simply comparing the memory address of the tokens. Since the interpreter only uses string equality operations for string comparison, simply checking for integer equality suffices for string comparison, speeding up the interpretation phase. Since the hash key is 4 bits long, this allows for reducing 4 searches in the binary tree compared to using a single binary tree.
Usage of jump hash tables for the special form evaluation procedure searches
There are 17 distinct procedures for evaluating the special forms in the Lisp interpreter,
define, if, quote, car, cdr, cons, atom, print, progn, while, {lambda, macro}, eval, eq, {+, -, *, /, mod}, {<, >}, list, and lambda/macro invocations (when if the token is not a special form). Using an if statement to find the corresponding procedure for a given token becomes a linear search for the token comparisons. To speed up this search process, a hash table is created for jumping to the corresponding procedures. Since the memory addresses for the special forms can be determined before parsing the Lisp program, all of the symbols for the special forms have a fixed memory address. Therefore, the hash key can be created by subtracting an offset to the symbol’s memory address, to point to a hashtable that is created near the register locations. This hashtable is provided in memheader.eir. When the hash key is larger than the regions of this hashtable, it means that the symbol is not a special form, so the evaluation jumps to the lambda/macro invocation procedure.
Usage of 2-bit headers to represent value types
The Lisp implementation has 3 distinct value types, ATOM, INT, and LAMBDA. Each value only consumes one QFT byte of memory; the ATOM value holds the pointer to the symbol’s string hashtable, the INT value holds the signed integer value, and LAMBDA holds a pointer to the Lambda struct, as well as its subtype information, of either LAMBDA, MACRO, TEMPLAMBDA and TEMPMACRO. (The TEMPLAMBDA and TEMPMACRO subtypes are lambda and macro types that recycles its argument value memory space every time it is called, but is unused in the final lisp programs.) Since the RAM’s address space is only 10 bits, there are 6 free bits that can be used for addresses holding pointers. Therefore, the value type and subtype information is held in these free bits. This makes the integer in the Lisp implementation to be a 14-bit signed integer, ranging from -8192 to 8191.
Minimization of Stack Region Usage
Since the C compiler used in this project does not have memory optimization features, this has to be done manually within the C source code. This led to the largest reason why the interpreter’s source code seems to be obfuscated.
One of the largest bottlenecks for memory access was stack region usage. Every time a stack region memory access occurs, the assembly code performs memory address offset operations to access the stack region. This does not happen when accessing the heap memory, since there is only one heap region used in the entire program, so the pointers for global variables can be hard-coded by the assembler. Therefore, it is favorable optimization-wise to use the heap memory as much as possible.
One way to make use of this fact is to use as much global variables as possible. Since registers and common RAM memory share the same memory space, global variables can be accessed with a speed comparable to registers (However, since the physical location of the RAM memory slot within the pattern affects the I/O signal arrival time, and the registers have the most smallest RAM addresses, i.e. they are the closest to the CPU unit, the registers have the fastest memory access time).
Another method of saving memory was to use union memory structures to minimize the stack region usage. In the C compiler used in this project, every time a new variable is introduced in a function, the function’s stack region usage (used per call) is increased to fit all of the variables. This happens even when two variables never appear at the same time. Therefore, using the fact that some variables never appear simultaneously, unions are used for every occurence of such variables, so that they can use a shared region within the stack space. This led to minimization of the stack region usage. Since the stack region is only 233 hextets (1 byte in the QFT RAM is 16 bits) large, this allowed to increase the number of nested function calls, especially the nested calls of eval which evaluates the S-expressions. Since the S-expressions have a list structure, and eval becomes nested when lambdas are called in the Lisp program, this optimization was significant for allowing more sophisticated Lisp programs to be run in the architecture.
The QFTASM layer
The QFT assembly generated by the C compiler has a lot of room for optimization. I therefore created a compiler optimization tool to reduce the QFTASM assembly size.
Constant folding
Immediate constant expressions such as ADD 1 2 destination is folded to a MOV operation.
MOV folding
The QFT assembly code can be splitted into subregions by jump operations, such that:
- Each subregion doesn’t contain any jump operations
- Each subregion ends with a jump operation
- Every jump operation in the assembly is guaranteed to jump to the beginning of a subregion, and never to the middle of any subregion
The last guarantee where jumps never occur in the middle of a subregion is provided by the C compiler. The ELVM assembly’s program counter is designed so that it increases only when a jump instruction appears. This makes an ELVM program counter to point to a sequence of multiple instructions, instead of a single instruction. Since the ELVM assembly uses the ELVM program counter for its jump instructions, it is guaranteed that the jump instructions in the QFT assembly never jump to the middle of any subregion, and always jumps to a beginning of a subregion.
In each subregion, the dependency graph for the memory address is created. If a memory address becomes written but is later overwritten without becoming used in that subregion at all, the instruction to write to that memory address is removed. Since it is guaranteed that jump operations never jump to the middle of any subregion, it is guaranteed that the overwritten values can be safely removed without affecting the outcome of the program. The MOV folding optimization makes use of this fact to remove unnecessary instructions.
This folding process is also done with dereferences; if a dereferenced memory address is written, and the address is overwritten without being used at all, and the dereference source is unoverwritten at all during this process, the instruction for writingto the dereferenced memory address is removed.
Jump folding
If the destination of a conditional or fixed-destination jump instruction points to another jump instruction with a fixed destination, the jump destination is folded to the latter jump instruction’s destination.
A similar folding is done when a fixed jump instruction points to a conditional jump instruction, where the fixed jump instruction is replaced by the latter conditional jump instruction.
The Varlife layer (the computer architecture)
Created the with a lookup table structure for the ROM module
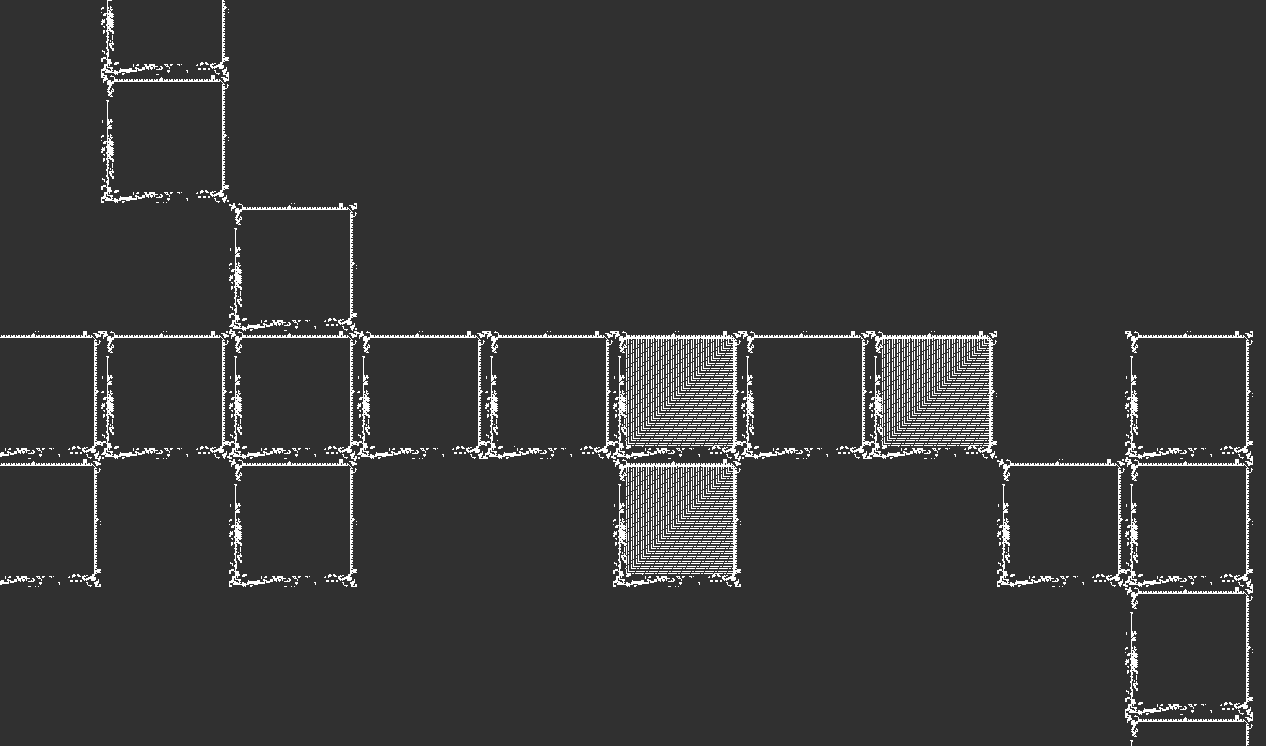
In this image of the CPU and its surrounding modules, the two modules on the top are the ROM modules. The original ROM module had one table, with the memory address as the key and the instruction as the value. I recreated the ROM module to add a lookup table layer, where each distinct instruction (not the opcodes, but the entire instruction including the values used within) holds a distinct serial integer key. The ROM module on the right accepts a program counter address and returns the instruction key for the program counter. The module on the left accepts the instruction key and returns the actual bits of the instruction as the output. This allows for dictionary compression to be performed to the ROM data, saving a lot of space. Since the instructions are 45 bits and the instruction keys are only 10 bits, the instruction key table is 1/4 the size of the original ROM module. Although the ROM size is 3223 for the entire Lisp interpreter, there were only 616 distinct instructions in the Lisp interpreter, making the size of the instruction table be 616 ROM units high, effectively reducing the ROM module size altogether.
The ROM module features another form of compression, where absence of cells are used to represent 0-valued bits within the instruction. Below is a close-up look of the ROM value module:

Notice that some cells on the left are absent, despite the table being expected to be a rectangular shape. This is because absent cells do not emit any signals, hence effectively emitting 0-valued bits as the output. To use this fact, all of the instructions are first alphabetically ordered at table creation time, so that instructions that start with trailing zeroes become located higher in the table (further from the signal source). This allows for a maximum number of cells to be replaced with absent units to represent 0-valued bits. In fact, the instruction for no-ops is represented as all zeroes, so all of the units in the value module are replaced by absent cells. The no-op instruction appears a lot of times immediately after the jump operation, due to the fact that the QFT architecture has a branch delay when invoking a jump instruction, requiring a no-op instruction to be present to compensate for the delay.
Added new optimized instructions to the ALU, and removed unused ones
I removed the AND, OR, SL (shift left), SRL (shift right logical), and the SRA (shift right arithmetical) opcodes, and added the SRU (shift right unit) and SRE (shift right eight) opcodes to the architecture. Since there already were opcodes for XOR (bitwise-xor) and ANT (bitwise-and-not), AND and OR, which were not used much in the interpreter, could be replaced by these opcodes. The bitshift operations had significantly larger patterns than the other opcodes, being more than 10 times larger than the other opcodes. These were reduced to a fixed-size shift operations which could be implemented in the same sizes as the other opcodes. Since the shift left opcode can be replaced by consecutively adding its own value, effectively multiplying by powers of 2, the opcode was safely removed. The main reason for the original bitshift units being large was due to the shift amounts being dependent on the values of the RAM. Converting a binary value to a physical (in-pattern) shift amount required a large pattern. On the other hand, shifting a fixed value could be implemented by a significantly more simpler pattern. The shift right eight instruction is mainly used for reading out the standard input, where each ASCII character in the input string is packed into one 16-bit RAM memory address.
This resulted in a total of exactly 8 opcodes, ANT, XOR, SRE, SRU, SUB, ADD, MLZ, and MNZ. Since this can fit in 3 bits, the opcode region for the instruction value was reduced by 1 bit. Since the RAM module is 10 bits, and the third value of the instruction is always the writing destination of the RAM, and the first instruction can also be made so that it becomes the reading source address of the RAM, this allows for an additional 6*2=12 bits to be reduced from the instruction length. These altogether has reduced the ROM word size from 58 to 45 bits, reducing nearly 1/4 of the original instruction size.
Extended the ROM and RAM address space from 9,7-bit to 12,10-bit
The original QFT architecture had a ROM and RAM address space of 9 and 7 bits. I extended the ROM and RAM address space to 12 and 10 bits, respectively. This was not a straightforward task as it first seemed, since the signal arrival timings between the modules had to be carefully adjusted in order for the signals to line up correctly. This involved reverse-engineering and experimenting undocumented VarLife pattern units used in the original QFT architecture. The same held for when redesigning other parts of the architecture.
Reducing the Standard Input Size
Since each byte of the RAM module can be ordered arbitrarily in the CPU’s architecture, the RAM is arranged so that the standard output is written at the very bottom of the RAM module, and proceeds upwards. Therefore, the contents of the RAM can easily be observed in a Game of Life viewer by directly examining the bottom of the RAM module.
Since RAM has 16 bits of memory per memory address, it allows to fit two ASCII-encoded characters per one address. Therefore, the standard input is read out by reading two characters per address. For the standard output, one character is written to one address for aesthetic reasons, so that the characters can be directly observed in a Game of Life viewer the pattern more easily. Also, for the standard output to proceed upwards within the RAM module pattern, the memory pointer for the standard output proceeds backwards in the memory space, while the pointer for the standard input proceeds forwards in the memory space.
The Game of Life layer
Optimizing the Game of Life layer mainly revolved around understanding the Macrocell format for representing and saving Game of Life patterns, and the Hashlife algorithm. The Macrocell format uses quadtrees and memoization for compressing repeated patterns. Since the final Game of Life pattern is an array of OTCA metapixels which are 2048x2048 large, and even has repeated patterns in the VarLife layer (meaning that there are repeated configurations of OTCA metapixels), this compression reduces the file size for the QFT pattern significantly. The best example that let me understand the Macrocell format was an example provided by Adam P. Goucher in this thread in Golly’s mailing list.
The Hashlife algorithm also uses quadtrees and memoization to speed up the Game of Life simulations. This algorithm makes use of the fact that the same pattern in a same time frame influences only a fixed extent of its surrounding regions, hence allowing for memoization.
As for optimization, I first noticed that the QFT pattern had a 1-pixel high pattern concatenated to the entire pattern. The original QFT pattern in the original QFT repository was carefully designed so that it is composed of 8x8-sized pattern units. Therefore, most of the patterns can be represented by 8x8 tiles. However, since the 1-pixel high pattern at the top creates an offset that shifts away the pattern from this 8x8 grid, it causes the pattern to have fewer repeated patterns if interpreted from the corner of its bounding box, causing the memoization to work inefficiently. I therefore tried putting a redundant cell (which does not interfere with the rest of the pattern) to realign the entire pattern to its 8x8 grid, which actually slightly reduced the resulting Macrocell file size from the original one. Although I didn’t compare the running times, since the Hashlife algorithm uses memoization over repeated patterns as well, I expect this optimization to at least slightly contribute to the performance of the simulation.
Another optimization was improving the metafier script used to convert VarLife patterns to Game of Life (MetafierV3.py). The original script used a square region to fit the entire pattern to create the quadtree representation. However, since the Lisp in Life VarLife pattern is 968 pixels wide but 42354 pixels high, it tried to allocate a 65536x65536-sized integer array, which was prohibitively large to run. I modified the script so that it uses a rectangular region, where absent regions of the quadtree are represented as absent cells. Although this is very straightforward with the knowledge of the Macrocell format, it was difficult at first until I became fond of the algorithms surrounding the Game of Life.
Memory Region Map and the Phases of Operation
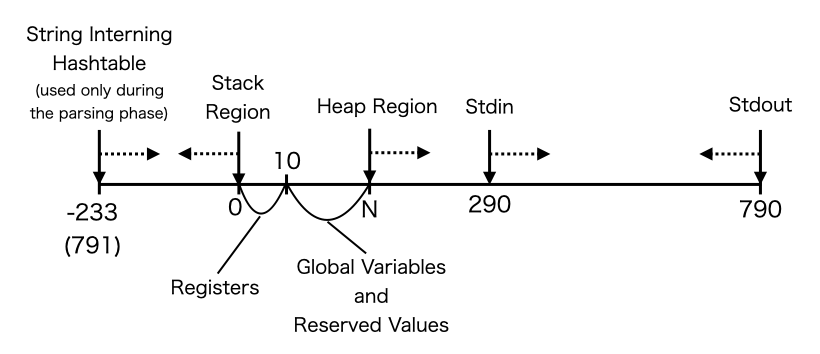
The memory region map is carefully designed to save space. This is best described with the operation phases of the interpreter.
Phase 0: Precalculations
Various precalculations are done after the interpreter starts running. The construction of the string interning hashtable for reserved atoms such as define, quote, etc. are done in this phase. For the GCC-compiled interpreter, some variables that are defined in the QFT memory header are defined in the C source.
Since the outcome of these precalculations are always the same for any incoming Lisp program, this phase is done on the host PC, and the results are saved as ramdump.csv during the QFTASM compile time. The results are then pre-loaded into the RAM when the VarLife and Game of Life patterns are created. This allows to saves some CPU cycles when running the interpreter.
As explained earlier, the QFT architecture holds register values in the RAM. There are 11 registers, which are placed in the addresses from 0 to 10.
The reserved values in the image include strings such as reserved atoms and the destinations of the jump hashtable used for evaluation. The rest of the region is used for storing global variables in the interpreter’s C source code.
Phase 1: Parsing
The Lisp program provided from the standard input is parsed into S-expressions, which is written into the heap region.
Notice that the string interning hashtables are created in the later end of the stack region. This is because these hashtables are only used during the parsing phase, and can be overwritten during the evaluation phase. For most Lisp programs including the ones in this repository, the stack region does not grow far enough to overwrite these values. This allows to place 3 growing memory regions during the parsing phase, the stack region used for nested S-expressions, the heap region which stores the parsed S-expressions, and the string interning hashtables when new strings are detected within the Lisp program. Newly detected strings such as variable names in the Lisp program are also written into the heap region.
The heap region is also designed so that it overwrites the standard input as it parses the program. Since older parts of the program can be discarded once it is parsed, this allows to naturally free the standard input region which save a lot of space after parsing. The standard input also gets overwritten by the Standard output if the output is long enough. However, due to this design, long programs may have trouble at parsing, since the input may be overwritten too far and get deleted before it is parsed. A workaround for this is to use indentation which places the program further ahead into the memory, which will prevent the program from being overwritten from the growing heap region. For all of the programs included in this repository, this is not an issue and the programs become successfully parsed.
Phase 2: Evaluation
By this time, all of the contents of the stack region and what is ahead of the head of the heap region can be overwritten in the further steps. Note that a similar issue with the standard input happens with the standard output - when too many Lisp objects are created during runtime, it may overwrite the existing standard output, or may simply exceed the heap region and proceed into the stack region. Since the heap region is connected to the later end of the stack region, this may be safe if the standard output is carefully handled, but the interpreter will eventually start overwriting values of the stack region if the heap continues to grow.
Miscellaneous
How can a 2-state OTCA Metapixel emulate the behavior of an 8-state VarLife pattern?
This is one of the most interesting ideas in the original QFT project to make the QFT architecture possible. As explained in the original QFT post, the 8 states of VarLife are actually a mixture of 4 different birth/survival rules with binary states. This means that each VarLife cell can only transition between two fixed states, and the birth/survival rule for that cell does not change at any point in time. Moreover, the OTCA Metapixel is designed so that each metapixel can carry its own birth/survival rules. Therefore, each VarLife cell can be enoded into an OTCA Metapixel by specifying its birth/survival rule and the binary state. This means that the array of OTCA Metapixels in the metafied pattern is actually a mixture of metapixels with different birth/survival rules, arranged in a way so that it makes the computation possible.
Halting Time
After the program counter is set to 65535 and the program exits, no more ROM and RAM I/O signals become apparent in the entire module. This makes the VarLife pattern becomes completely stationary, where every pattern henceforth becomes completely identical. Defining this as the halting time for the calculation, the pattern for print.lisp halts at exactly 105,413,068 VarLife generations.
The halting time for the Game of Life patterns are defined similarly for the meta-states of the OTCA Metapixels. Since OTCA Metapixels never become stationary, the Game of Life states do not become stationary after the halting time, but the meta-states of the OTCA Metapixels will become stationary after the halting time.
For the VarLife pattern of print.lisp, by generation 105,387,540, the value 65535 gets written to the program counter. At generation 105,413,067, the last signal becomes just one step from disappearing, and at generation 105,413,068 and onwards, the pattern becomes completely stationary and every pattern becomes identical to each other. In the Game of Life version, since the OTCA Metapixel continues running indefinitely, the pattern does not become completly stationary, but the meta-states of the OTCA Metapixels will become completely stationary, since it is an emulation of the VarLife pattern. Note that the halting times for programs other than print.lisp is just a sufficient number of generations, and not the exact values.
The required number of generations per CPU cycle depends on many factors such as the ROM and RAM addresses and the types of opcodes, since the arriving times of the I/O signals depend on factors such as these as well. This makes the number of generations required for the program to halt become different between each program. For example, print.lisp has a rate of 23822.16 generations per CPU cycle (GpC), but z-combinator.lisp has a rate of 28870.81 GpC, and primes-print.lisp has 31502.43 GpC. 23822.16 GpC is in fact insufficient for z-combinator.lisp to finish running, and 28870.81 is also insufficient for primes-print.lisp to finish running.
Miscellaneous Screenshots
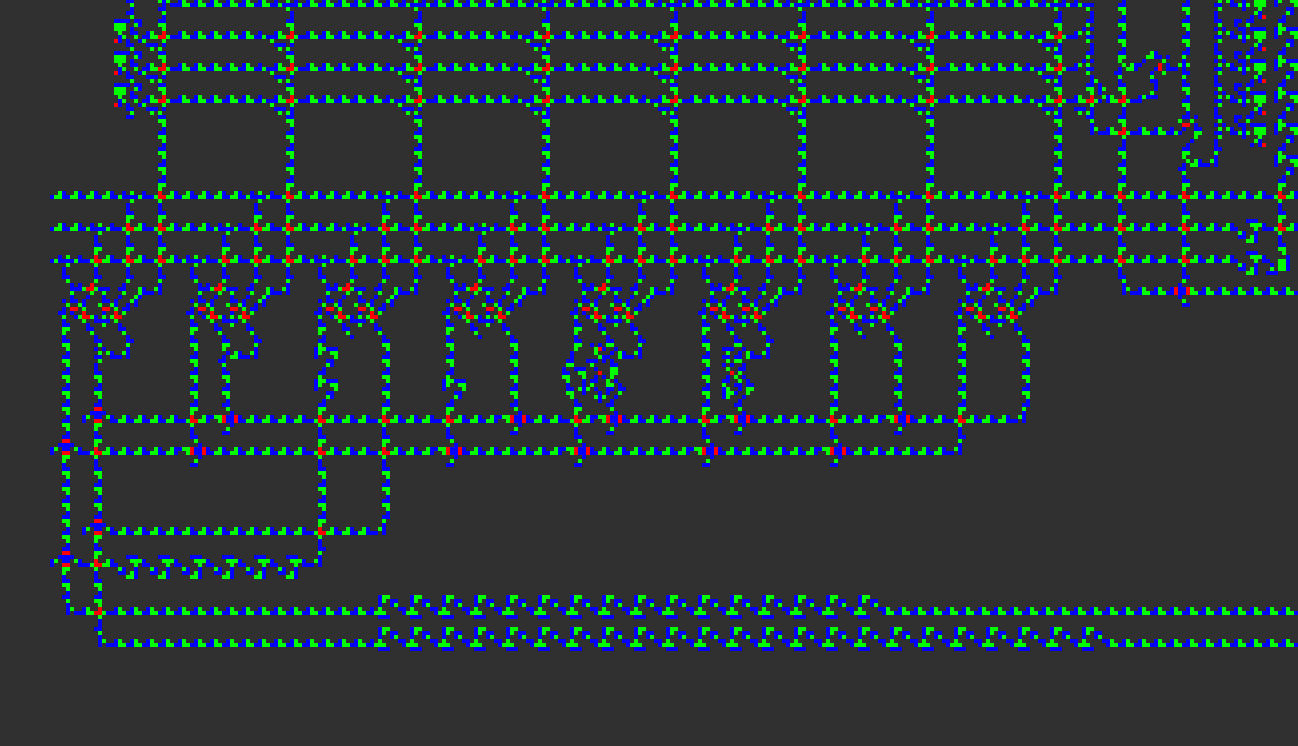
The ALU unit in the CPU. From the left are the modules for the ANT, XOR, SRE, SRU, SUB, ADD, MLZ, and the MNZ opcodes.
The SRE and the SRU opcodes were newly added for this project.
Credits
The CPU architecture used in this project was originally created by the members of the Quest For Tetris (QFT) project, and was later optimized and modified by Hikaru Ikuta for the Lisp in Life project. The VarLife cellular automaton rule was also defined by the members of the QFT project. The metafier for converting VarLife patterns to Conway’s Game of Life patterns was written by the members of the QFT project, and was later modified by Hikaru Ikuta to support the pattern size of the Lisp in Life architecture. The assembly language for the QFT architecture, QFTASM, was also originally designed by the members of the QFT project, and was later modified by Hikaru Ikuta for this project for achieving a feasible running time. The Lisp interpreter was written by Hikaru Ikuta. The compilation of the interpreter’s C source code to the ELVM assembly is done using an extended version of 8cc written by Rui Ueyama from Google. The compilation from the ELVM assembly to QFTASM is done by an extended version of ELVM (the Esoteric Language Virtual Machine), a project by Shinichiro Hamaji from Preferred Networks, Inc. The Game of Life backend for ELVM was written by Hikaru Ikuta, and was later further extended by Hikaru for the Lisp in Life project.
